Anna University
Numerical Methods
UNIT-II
INTERPOLATION AND APPROXIMATIONT
Two Marks With Answers
1. Explain briefly Interpolation.
Ans: Interpolation is the process of computing the values of a function for any value of the independent variable within an interval for which some values are given.
2. Definition of Interpolation and extrapolation.
Ans: Interpolation: It is the process of finding the intermediate values of a function from a set of its values specific points given in a tabulated form. The process of computing y corresponding to x is interpolation.
Extrapolation: If then the process is called extrapolation.
3. State Newton’s Forward interpolation formula.
4. State Newton’s Backward interpolation formula.
5. Error in Newton’s forward:
6. Error in Newton’s Backward:
7. State Newton’s divided difference formula.
8. Show that the divided differences are symmetrical in their arguments.
9. Show that divided difference operator is linear.
10. Divided difference table:
| X | Y | |||
| X0
X1 X2 X3
| Y0
Y1 Y2 Y3 |
11. Write Lagrangian’s polynomial formula.
12. What is the assumption we make when Lagrange’s formula is used?
Ans: It can be used whether the values of x, the independent variable are equally spaced or not whether the difference of y become smaller or not.
13. Write Lagrangian inverse interpolation formula.
14. Define Cubic Spline
Ans: Let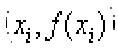
A cubic spline function f(x) w.r.t. the points x0, x1, .....xn is a polynomial of degree three in each interval (xi-1, xi) i = 1, 2, ...n such that ,
and
are continuous.
15. Write down the formula of Cubic Spline.
(OR)


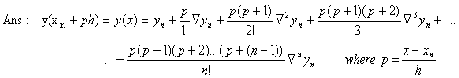



















No comments:
Post a Comment