Digital Logic Circuits - Analysis of Sequential Circuits

Analysis of Sequential Circuits

The behaviour of a sequential circuit is determined from the inputs, the outputs and the states of its flip-flops. Both the output and the next state are a function of the inputs and the present state.

The suggested analysis procedure of a sequential circuit is set out in Figure 6 below.

Figure 6. Analysis procedure of sequential circuits.

We start with the logic schematic from which we can derive excitation equations for each flip-flop input. Then, to obtain next-state equations, we insert the excitation equations into the characteristic equations. The output equations can be derived from the schematic, and once we have our output and next-state equations, we can generate the next-state and output tables as well as state diagrams. When we reach this stage, we use either the table or the state diagram to develop a timing diagram which can be verified through simulation.

This example is taken from D. D. Gajski, Principles of Digital Design, Prentice Hall, 1997, p.230.

Example 1.1. Modulo-4 counter

Derive the state table and state diagram for the sequential circuit shown in Figure 7.

Figure 7. Logic schematic of a sequential circuit.

SOLUTION:

STEP 1:     First we derive the Boolean expressions for the inputs of each flip-flops in the schematic, in terms of external input Cnt and the flip-flop outputs Q1 and Q0. Since there are two D flip-flops in this example, we derive two expressions for D1 and D0:

D0 = CntQ0 = Cnt'*Q0 + Cnt*Q0'

D1 = Cnt'*Q1 + Cnt*Q1'*Q0 + Cnt*Q1*Q0'

These Boolean expressions are called excitation equations since they represent the inputs to the flip-flops of the sequential circuit in the next clock cycle.

STEP 2:     Derive the next-state equations by converting these excitation equations into flip-flop characteristic equations. In the case of D flip-flops, Q(next) = D. Therefore the next state equal the excitation equations.

Q0(next) = D0 = Cnt'*Q0 + Cnt*Q0'

Q1(next) = D1 = Cnt'*Q1 + Cnt*Q1'*Q0 + Cnt*Q1*Q0'

STEP 3:     Now convert these next-state equations into tabular form called the next-state table.

Present State Q1Q0	Next State Cnt = 0 Cnt = 1
0 0 0 1 1 0 1 1	0 0 0 1 0 1 1 0 1 0 1 1 1 1 0 0

Each row is corresponding to a state of the sequential circuit and each column represents one set of input values. Since we have two flip-flops, the number of possible states is four - that is, Q1Q0 can be equal to 00, 01, 10, or 11. These are present states as shown in the table.

For the next state part of the table, each entry defines the value of the sequential circuit in the next clock cycle after the rising edge of the Clk. Since this value depends on the present state and the value of the input signals, the next state table will contain one column for each assignment of binary values to the input signals. In this example, since there is only one input signal, Cnt, the next-state table shown has only two columns, corresponding to Cnt = 0 and Cnt = 1.

Note that each entry in the next-state table indicates the values of the flip-flops in the next state if their value in the present state is in the row header and the input values in the column header.

Each of these next-state values has been computed from the next-state equations in STEP 2.

STEP 4:     The state diagram is generated directly from the next-state table, shown in Figure 8.

Figure 8. State diagram

Each arc is labelled with the values of the input signals that cause the transition from the present state (the source of the arc) to the next state (the destination of the arc).

In general, the number of states in a next-state table or a state diagram will equal 2^m , where m is the number of flip-flops. Similarly, the number of arcs will equal 2^m x 2^k , where k is the number of binary input signals. Therefore, in the state diagram, there must be four states and eight transitions. Following these transition arcs, we can see that as long as Cnt = 1, the sequential circuit goes through the states in the following sequence: 0, 1, 2, 3, 0, 1, 2,....  On the other hand, when Cnt = 0, the circuit stays in its present state until Cnt changes to 1, at which the counting continues.

Since this sequence is characteristic of modulo-4 counting, we can conclude that the sequential circuit in Figure 7 is a modulo-4 counter with one control signal, Cnt, which enables counting when Cnt = 1 and disables it when Cnt = 0.

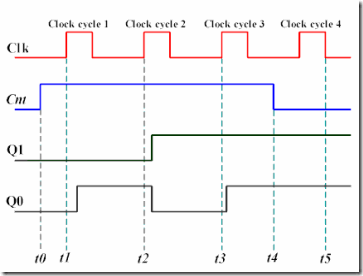
Below, we show a timing diagram, representing four clock cycles, which enables us to observe the behaviour of the counter in greater detail.

Figure 9. Timing Diagram

In this timing diagram we have assumed that Cnt is asserted in clock cycle 0 at t₀ and is disasserted in clock cycle 3 at time t₄. We have also assumed that the counter is in state Q1Q0 = 00 in the clock cycle 0. Note that on the clock's rising edge, at t₁, the counter will go to state Q1Q0 = 01 with a slight propagation delay; in cycle 2, after t₂, to Q1Q0 = 10; and in cycle 3, after t₃ to Q1Q0 = 11. Since Cnt becomes 0 at t₄, we know that the counter will stay in state Q1Q0 = 11 in the next clock cycle.

In Example 1.1 we demonstrated the analysis of a sequential circuit that has no outputs by developing a next-state table and state diagram which describes only the states and the transitions from one state to the next. In the next example we complicate our analysis by adding output signals, which means that we have to upgrade the next-state table and the state diagram to identify the value of output signals in each state.

This example is taken from D. D. Gajski, Principles of Digital Design, Prentice Hall, 1997, p.234.

Example 1.2

Derive the next state, the output table and the state diagram for the sequential circuit shown in Figure 10.

Figure 10. Logic schematic of a sequential circuit.

SOLUTION:

The input combinational logic in Figure 10 is the same as in Example 1.1, so the excitation and the next-state equations will be the same as in Example 1.1.

Excitation equations:

D0 = CntQ0 = Cnt'*Q0 + Cnt*Q0'

D0 = Cnt'*Q1 + Cnt*Q1'*Q0 + Cnt*Q1*Q0'

Next-state equations:

Q0(next) = D0 = Cnt'*Q0 + Cnt*Q0'

Q1(next) = D0 = Cnt'*Q1 + Cnt*Q1'*Q0 + Cnt*Q1*Q0'

In addition, however, we have computed the output equation.

Output equation: Y = Q1Q0

As this equation shows, the output Y will equal to 1 when the counter is in state Q1Q0 = 11, and it will stay 1 as long as the counter stays in that state.

Next-state and output table:

Present State Q1 Q0	Next State Cnt=0 Cnt=1	Output Z
0 0 0 1 1 0 1 1	0 0 0 1 0 1 1 0 1 0 1 1 1 1 0 0	0 0 0 1

State diagram:

Figure 11. State diagram of sequential circuit in Figure 10.

Timing diagram:

Figure 12. Timing diagram of sequential circuit in Figure 10.

Note that the counter will reach the state Q1Q0 = 11 only in the third clock cycle, so the output Y will equal 1 after Q0 changes to 1. Since counting is disabled in the third clock cycle, the counter will stay in the state Q1Q0 = 11 and Y will stay asserted in all succeeding clock cycles until counting is enabled again.

Design of Sequential Circuits

The design of a synchronous sequential circuit starts from a set of specifications and culminates in a logic diagram or a list of Boolean functions from which a logic diagram can be obtained. In contrast to a combinational logic, which is fully specified by a truth table, a sequential circuit requires a state table for its specification. The first step in the design of sequential circuits is to obtain a state table or an equivalence representation, such as a state diagram.

A synchronous sequential circuit is made up of flip-flops and combinational gates. The design of the circuit consists of choosing the flip-flops and then finding the combinational structure which, together with the flip-flops, produces a circuit that fulfils the required specifications. The number of flip-flops is determined from the number of states needed in the circuit.

The recommended steps for the design of sequential circuits are set out below.

.State Reduction

Any design process must consider the problem of minimising the cost of the final circuit. The two most obvious cost reductions are reductions in the number of flip-flops and the number of gates.

The number of states in a sequential circuit is closely related to the complexity of the resulting circuit. It is therefore desirable to know when two or more states are equivalent in all aspects. The process of eliminating the equivalent or redundant states from a state table/diagram is known as state reduction.

Example: Let us consider the state table of a sequential circuit shown in Table 6.

Table 6. State table

Present State	Next State x = 0 x = 1	Output x = 0 x = 1
A B C D E F	B C F D D E F E A D B C	1 0 0 0 1 1 0 1 0 0 1 0

It can be seen from the table that the present state A and F both have the same next states, B (when x=0) and C (when x=1). They also produce the same output 1 (when x=0) and 0 (when x=1). Therefore states A and F are equivalent. Thus one of the states, A or F can be removed from the state table. For example, if we remove row F from the table and replace all F's by A's in the columns, the state table is modified as shown in Table 7.

Table 7. State F removed

Present State	Next State x = 0 x = 1	Output x = 0 x = 1
A B C D E	B C A D D E A E A D	1 0 0 0 1 1 0 1 0 0

It is apparent that states B and E are equivalent. Removing E and replacing E's by B's results in the reduce table shown in Table 8.

Table 8. Reduced state table

Present State	Next State x = 0 x = 1	Output x = 0 x = 1
A B C D	B C A D D B A B	1 0 0 0 1 1 0 1

The removal of equivalent states has reduced the number of states in the circuit from six to four. Two states are considered to be equivalent if and only if for every input sequence the circuit produces the same output sequence irrespective of which one of the two states is the starting state.