Digital Logic Circuits–Encoder and Decoder

Decoder

A decoder is a multiple-input, multiple-output logic circuit that converts coded inputs into coded outputs, where the input and output codes are different.Binary Decoder has n inputs and 2ⁿoutputs also called as n-to-2ⁿ decoder. Inputs have all the 2ⁿ combinations and the corresponding output will be activated for each input combinations.Decoding is necessary in applications such as data multiplexing, 7 segment display and memory address decoding. Enable inputs must be on for the decoder to function, otherwise its outputs assume a single "disabled" output code word. Figure below shows the pseudo block of a decoder.

A binary decoder has n inputs and 2ⁿ outputs. Only one output is active at any one time, corresponding to the input value. Figure below shows a representation of Binary n-to-2ⁿ decoder

 e.g. 3-to-8 decoder has 3 inputs and 8 outputs

3-to-8 Decoder

Function Table

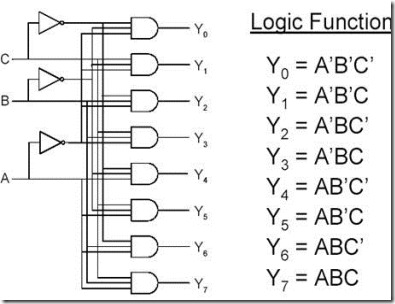
3-to-8 Decoder Logic Circuit

2-to-4 Decoder with Output Enable

Implement Logic Function with Decoder

• Any n-variable logic function, in canonical sum-of-minterms form can be implemented using a single n-to-2ⁿ decoder to generate the minterms, and an OR gate to form the sum.
• The output lines of the decoder corresponding to the minterms of the function are used as inputs to the or gate.
• Any combinational circuit with n inputs and m outputs can be implemented with an n-to-2ⁿ decoder with m OR gates.

Suitable when a circuit has many outputs, and each output function is expressed with few minterms.

(Ex) Full adder using decoder

S(x, y, z) = (1,2,4,7)

C(x, y, z) = (3,5,6,7)

Truth Table

X	Y	Z	C	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

From the truth table we know the values for which the sum (s) is active and also the carry (c) is active. Thus we have the equation as shown above and a circuit can be drawn as shown below from the equation derived.

Use a 3-to-8 decoder to implement:

f = x’y’z + xy’z + xyz

(m1 + m5 + m7)

MSI Decoders

1. 2-to-4 Decoder
2. 3-to-8 Decoder
3. 4-to-16 Decoder
4. BCD-to-Decimal Decoder
5. BCD-to-Seven-Segment Decoder

e.g. Low Power Schottky TTL:

74LS138 3-to-8 Decoder where G1, G2A and G2B are enable pins

Logic Symbol

74LS138 3-to-8 Decoder

Implement Logic Function with74LS138

Use a 3-to-8 decoder to implement:

f = x’y’z + xy’z + xyz

(m1 + m5 + m7)

4-to-16 Decoder

Use 2 3-to-8 decoders

Inputs: D, C, B, A

Outputs: Y0 – Y15

When D = 0, top decoder is enabled

When D = 1,bottom decoderis enabled

En’ is enable

Binary Encoders

An encoder is a combinational circuit that performs the inverse operation of a decoder. If a device output code has fewer bits than the input code has, the device is usually called an encoder. e.g. 2ⁿ-to-n, priority encoders.

The simplest encoder is a 2ⁿ-to-n binary encoder, where it has only one of 2ⁿ inputs = 1 and the output is the n-bit binary number corresponding to the active input. It can be built from OR gates

e.g. 4-to-2 Encoder

Octal-to-Binary Encoder

Octal-to-Binary take 8 inputs and provides 3 outputs, thus doing the opposite of what the 3-to-8 decoder does. At any one time, only one input line has a value of 1. The figure below shows the truth table of an Octal-to-binary encoder.

Truth Table

I0	I1	I2	I3	I4	I5	I6	I7	Y2	Y1	Y0
1	0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	0	0	0	1	0
0	0	0	1	0	0	0	0	0	1	1
0	0	0	0	1	0	0	0	1	0	0
0	0	0	0	0	1	0	0	1	0	1
0	0	0	0	0	0	1	0	1	1	0
0	0	0	0	0	0	0	1	1	1	1

For an 8-to-3 binary encoder with inputs I0-I7 the logic expressions of the outputs Y0-Y2 are:

Y0 = I1 + I3 + I5 + I7

Y1= I2 + I3 + I6 + I7

Y2 = I4 + I5 + I6 +I7

Based on the above equations, we can draw the circuit as shown below

Priority Encoder

If more then two inputs are active simultaneously, the output is unpredictable or rather it is not what we expect it to be.This ambiguity is resolved if priority is established so that only one input is encoded, no matter how many inputs are active at a given point of time. The priority encoder includes a priority function. The operation of the priority encoder is such that if two or more inputs are active at the same time, the input having the highest priority will take precedence.

e.g. 4-to-2 PriorityEncoder

A3 has the highest priority

A0 has the lower priority

74148 8-to-3 Priority Encoder

16-to-4 Priority Encoder

Cascade two 74148 8-to-3 priority encoders. The Input 15 has highest priority